Home • People • Courses • Program • Research • Clinic • Goals • Kiosk • News
Understanding Basic Statistics • Fitting • Exercise • Excel • Igor • Kaleidagraph • Origin • Power Laws • Dimensional Analysis
When one quantity (say y) depends on another (say x) raised
to some power, we say that y is described by a power law. For
example, the distance traveled by an object in free fall (in the absence
of air resistance) is given by
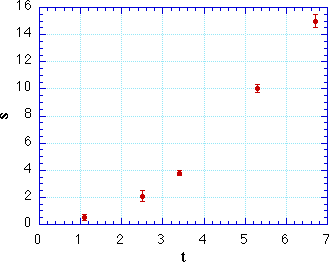Ignoring the dependence on g, this equation says that s is
proportional to the square of t. Plotting on linear (Cartesian)
axes produces a parabola. Now, a parabola is a very beautiful curve, but
it is difficult to eyeball a curve and say with confidence that it is
a parabola. It is even harder to eyeball some data points, with their
uncertainties, and tell whether they follow a parabolic curve.
Eyeballs are much happier with straight lines.
There is a handy way to convert this power-law relationship into a straight
line; just take the logarithm of both sides of the equation:
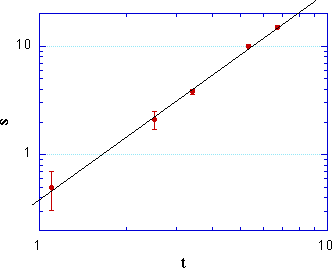If we plot log(s) on the y axis and log(t) on the
x axis, we get a straight line with slope 2 (which is the exponent
of t). Using Kaleidagraph or Origin you can just double-click
the axes to convert the display from linear to logarithmic. You can also
perform a proper c2 fit, as described on the Fitting page.
Understanding Basic Statistics •
Fitting •
Exercise •
Excel •
Igor •
Kaleidagraph •
Origin •
Power Laws •
Dimensional Analysis
 |
Copyright ©
Harvey Mudd College Physics Department 241 Platt Blvd., Claremont, CA 91711 909-621-8024 http://www.physics.hmc.edu/ WebMaster (at) physics.hmc.edu Last modified: 26 August 2012 |