- Draw as many diagrams of the situation described in the problem
statement as are necessary to make the situation and your analysis
clear. Often, one will suffice. On your diagrams, use symbols
not values. Near the diagram, draw up a table of the givens,
being sure to respect the precision and units
given in the problem statement.
- Read the entire question or problem as many times as necessary to be
confident that you now precisely what is being asked in each section. Make a
mental note whether the same intermediate quantity will figure in several
calculations. If not, numerical values should only be substituted into
completely derived algebraic expressions for the requested quantities.
- In force problems, isolate the appropriate components of the system and
sketch a force diagram for them. Put a coordinate system on each
diagram. Deduce the appropriate equations of motion.
In other problems, cite the appropriate laws and relations, and
justify the equations you deduce where necessary. Be certain
that all symbols you use have been defined, either by context or explicitly.
- Complete the algebra using symbols; outline your formula. If no values have
been provided, check your formula using dimensional analysis. If values have
been provided, substitute them into the formula, being sure to respect their
precision and units. Compute the requested value. Round your answer to the
precision of the least precise given value upon which your result depends. In
cases where a given is written as 800 km, for example, use 1, 2, or 3
significant figures based on the precision of the other given values. Be
sure that the units work out. Outline the final (rounded) answer written
in appropriate units. An answer of 1.0 x 107 s should
often be converted to 120 days or 3.8 months to make the answer more
meaningful or useful.
In subsequent calculations, use unrounded values and round
at the end.
Most importantly, ask yourself, "Does the answer make
sense?"
- Look at your answers and ask if they make physical sense. If they don't, go
back over the calculation. Check the formula to be sure that it displays the
appropriate dependencies on the givens. Should the velocity increase or
decrease with time? As
goes to zero or 
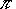/2, does
your formula simplify properly? etc. Finally and most importantly, ask
yourself what you have learned.
Sample Problem
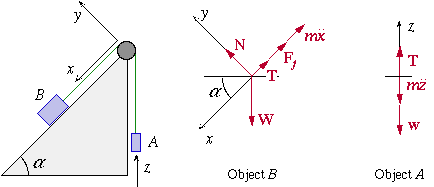
Halliday, Resnick, and Krane, 6-26, p. 125.Object B weighs 94.0 lb and object A weighs 29.0 lb. Between object B and the plane the coefficient of static friction is 0.56 and coefficient of kinetic friction is 0.25. (a) Find the acceleration of the system if B is initially at rest. (b) Find the acceleration if B is moving up the plane. (c) What is the acceleration if B is moving down the plane? The plane is inclined by 42.0°.
W = 94.0 lb uk = 0.25 w = 29.0 lb us = 0.56 [[alpha]] = 42.0deg.
From the force diagram for A, we get the equation
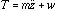
From the force diagram for B, we get the pair of equations
.
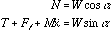If we assume that the string is inextensible, then
.
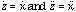We further assume that the string and pulley are massless, and that the pulley
is frictionless. Then the tension appearing the the first and third equations
is the same.
(a) The frictional force must be less than or equal to the product of the
normal force and the coefficient of static friction, us, for the object
to remain at rest. Let us calculate u assuming the objects remain at
rest to determine whether this is less than the given value. Substituting
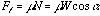in the third equation gives
,
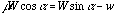which simplifies to
.
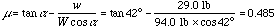Since u < us, the objects remain at rest.
(b) If B is initially moving up the plane, then the sense of the frictional force is opposite to that indicated in the diagram. We can solve for either case by writing the third equation as
,
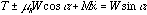where the upper sign corresponds to the case of motion down the plane, and the lower sign to motion up the plane. Solving for the acceleration gives
,
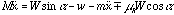which simplifies to
.
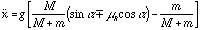This clearly has the right dimensions. Plugging in numbers and using g = 32.2 ft s-2 gives
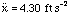
for motion up the plane, and
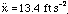
for motion down the plane. These values have been rounded to 3 significant figures, in agreement with the given information. Is it reasonable that the acceleration for motion down the plane is greater? Yes, because while friction opposes the motion in both cases, gravity opposes the motion in the former case and drives it in the latter. Furthermore, based on our choice of coordinate system as indicated on the first sketch, the acceleration is down the plane, as it must be.
