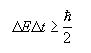
In his most famous paper, "Particle Creation by Black Holes" (1975), Hawking described a process by which black holes actually radiate particles. Not surprisingly, the theory was not initially well received. Hawking's discovery followed from a debate at the time about the thermodynamics of black holes. A while before his derivation of black hole radiation, Hawking himself proved what is now known as the Area Theorem of black holes, which states that the surface area of a black hole can never decrease. If several black holes are present, it is the sum of the surface areas that can never decrease. The theorem looked very much like the second law of thermodynamics, which states that entropy must always increase. The second law of thermodynamics proved to be a bit of a problem for the theory of black holes, as the theory did not provide an equilibrium state for a black hole. A black hole in a radiation bath would continually absorb radiation and never come to equilibrium. This is seemingly a problem, as black holes would then be an entropy sink. If an object of some entropy fell into a black hole, then the entropy of our universe would be decreased, which violates the second law. One might conjecture that the black hole has some entropy beyond the event horizon, but we can never know how much because we are entirely disconnected from the world inside the event horizon. Jacob Bekenstein followed this debate with the hypothesis that the area of the event horizon was a measure of the entropy. If some mass was thrown into the black hole, the area would increase and therefore, so would the black hole's entropy. The problem was that if the black hole had an observable entropy, then it would also have a temperature. No one wanted to accept that black holes had a temperature, because they would then have to emit radiation, which went against the very definition of a black hole.
Hawking undertook the task of applying quantum mechanics to black hole dynamics. While his formulation is beyond the scope of this web page, a slightly quantitative and highly qualitative examination of the problem can yield a very good picture of what Hawking discovered. Hawking first attempted to examine the space-time outside the black hole using quantum field theory, which has a very different picture of empty space than the classical definition. His first step was to consider what happens when any field (for example, the electromagnetic field) is quantized in the space-time exterior to a black hole. The quantum mechanical description of a vacuum is space seething with virtual particles and antiparticles whose presence cannot be detected directly. The exact description involves two Hermitian operators, the annihilation and creation operators. Again, the exact formulation is beyond the scope of our treatment of the subject. Nevertheless, a good qualitative interpretation can be obtained by considering the energy-time form of the Heisenberg uncertainty principle:
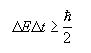
7 which states that the product of the uncertainty in the energy and the uncertainty in the time is on the order of h-bar. If we restrict ourselves to very short time scales, the uncertainty in the energy can be very large. In the intermediate stage of virtual pair production, conservation of energy appears to have been violated. This is where the uncertainty principle comes to the rescue, as the particles are created and annihilated on such short time scales as to agree with the uncertainty relation above. When we take delta-t to be large, energy is conserved as we could never have observed the particles in the intermediate stage.
At first glance, this process of virtual particle creation may seem a little phony. With that in mind, we can consider the more tangible case of electric field particle creation. This process can actually be observed by applying a strong electric field across a capacitor in a vacuum:
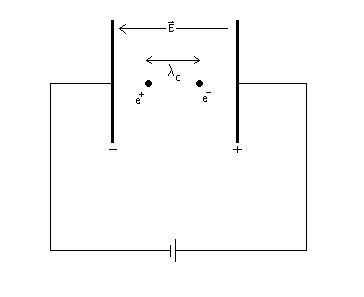
The quantum mechanical description of the vacuum allows for the creation of the particle/antiparticle pairs, and the electric field tends to separate the charges. If the field is strong enough, the particles tunnel through the quantum barrier and materialize as real particles. The field necessary to accomplish this feat is achieved when the work done to separated the charges by a Compton wavelength equals the energy necessary to create the particles:
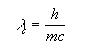
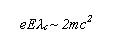
It should be noted that conservation of energy is not violated, as the energy it took to create the particles would be precisely equal to the decrease in the energy of the weakened electric field.
So far we have not introduced the possibility of a charged black hole, and will only consider an uncharged, non-rotating black hole. The logical next question is, if there is no electric field outside the black hole, how can these virtual particle/antiparticle pairs be of any consequence to black holes? The answer is that if a virtual particle pair is created very near to the event horizon, one of the particles could fall the black hole while one escapes to infinity:
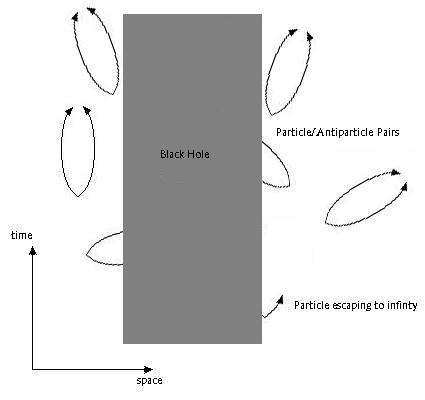
To an outside observer, it looks as if the black hole as radiated a particle. Indeed, to conserve energy, the energy it took to create the particle and shoot it off to infinity must have come from the black hole. The particle that did not escape must have had the vexing property of negative energy. This is what happens when a system messes around with particles that classically were not supposed to be created. When looking at the entire system, the total energy of the black hole has decreased and therefore, by Einstein's famous relation, the mass must have decreased. This is the process by which black holes radiate, which is now known as Hawking radiation.