![]()
If the black hole is losing mass, then by equation (1), its Schwarzschild radius must be decreasing. This equates to a decrease in the surface area of the event horizon. This would seem to violate Hawking's own area theorem, which states that the area can never decrease. The area theorem of general relativity gets replaced by a second law of thermodynamics for black holes, which states that the sum of the entropies of the black hole and the matter outside the black hole never decreases. While emitting a particle decreases the entropy of the black hole, the materialized particle has its own entropy that when summed together, equals or exceeds the initial entropy.
In the case of the electric field particle creation, the electric field strength necessary to create the particles was on the order of the particleās Compton wavelength. In the case of the black hole, the particles are created when their Compton wavelength is on the order of the Schwarzschild radius. Since the Compton wavelength goes as one over the mass of the particle, the larger the black hole the less massive its radiated particles must be. This argument must be modified for massless particles, as they have no barrier to penetrate. The production rate of massless particles is controlled by the phase space available to them. Along these lines, it is possible to equate the mean separation of blackbody photons, hc/kT , to the Schwarzschild radius, obtaining an estimate of the black holeās temperature:
![]()
In the case of black holes of mass M > 10^14 kilograms, the temperature is sufficiently low that the only quanta the hole can emit are those with zero rest mass: neutrinos (which we shall assume are truly massless), photons, and gravitons.
Now it is possible to examine the properties of radiating black holes. Starting only with the estimate for the temperature of a black hole in equation (9), one can take the black hole to be a perfect blackbody that should radiate energy according to Stefanās Law, which states that the flux of radiation is given by:
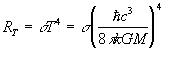
where sigma is the Stefan-Boltzmann constant. The quantity above has units of watts per square meter. We want to know the energy output of the black hole, which we obtain by integrating equation (10) over the surface of the black hole. The surface area of a black hole is:
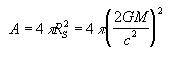
It is easily shown that the energy output of the black hole is:
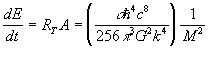
All of the terms on the right hand side of (12) are constants except the 1/M^2 factor. Using E = Mc^2, we can modify (12) to yield:
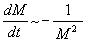
where the minus sign comes from the fact that the black hole is losing mass. This is a very interesting differential equation, and gives an idea as to what the mass loss will look like:
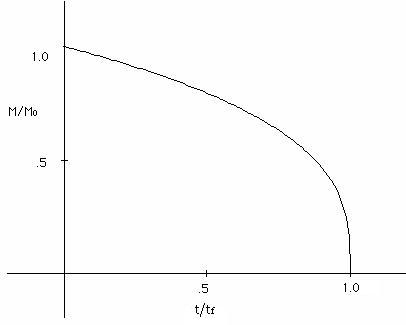
Separating variables and integrating, one finds that the lifetime of the black hole goes as the cube of the mass:
Collecting the various constants, a more helpful interpretation of (14) gives:
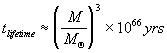
where is a solar mass. Clearly, for black holes on the order of a solar mass, Hawking radiation is of no consequence. However, during the Big Bang, the Universe underwent severe density fluctuations, which might have been capable of creating "mini" black holes with masses many orders of magnitude less than the black holes that are created today. Those with masses much less than 10^12 kg would have exploded by now, and those on the order of 10^12 kg would have lifetimes comparable with the current age of the Universe (~15 billion years).
One can get a feel for what such a primordial black hole would "look" like by examining a black hole with an initial mass of ~ 10^12 kg. The only assumptions needed are that (1) the Universe is ~15 billion years old, (2) the black hole is non-rotating and uncharged, and (3) the black hole has incurred no increase in mass. The Cosmic Microwave Background Radiation in which the black hole has been bathed for the extent of its lifetime can also be neglected. The evaporation time for such a black hole is around 20 billion years. This would give it a current mass of ~5 * 10^11 kg (about half of its initial mass). Using eq. (9), we obtain a surface temperature of about 2 * 10^11 K! This black hole is anything but black, as by eq. (12), it is emitting ~1500 megawatts of power. Considering the incredible surface temperature, this may even seem a little small. However, the Schwarzschild radius for such a black hole is less than a fermi, and to obtain the power we must integrate the luminosity over the surface area. This accounts for the relatively small power output of such a hot object, as the surface area is on the order of 10^-30 m^2. By using Wien's displacement law:
we find that the blackbody spectrum peaks around a wavelength of 10^-14 m, which is in the gamma ray spectrum.