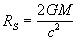
Before addressing black hole radiation, some general facets of black hole dynamics must be introduced. Standard model black holes are formed when large-mass stars (>3 solar masses) run out of nuclear fuel in their core and collapse due to their extreme "pull" of gravity. For stars with masses less than this, either neutron or electron degeneracy pressure is enough to fight the force of gravity. At the three-solar-mass limit however, there is no known force that is strong enough to stave of the complete collapse of the star into a black hole. Here is an animation of a black hole collapse (courtesy of Maple) that demonstrates the "rubber sheet" analogy of general relativity. The cutoff at the bottom is the event horizon, at which point all "lines" that enter it do not come back out. All of the mass that does collapse must coalesce into a single point, known as a singularity. There is no quantum theory of gravity as of yet, and the current state of physics cannot explain the extreme conditions at the center of a black hole.
As John Michell noted over two hundred years ago, one can imagine an object so massive and dense that the escape velocity at the surface is equal to the speed of light. Using simple Newtonian physics, we can solve for the radius of such an object by setting the kinetic energy of particle traveling at the speed of light equal to the gravitational potential energy at a particular R away from the center of the object. The mass of the particle cancels on both sides, and by solving for R we obtain:
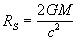
This is known as the characteristic Schwarzschild radius. It is named after Karl Schwarzschild who, less than a month after the publication of Einstein's general theory of relativity, derived the solution for the gravitational field surrounding a spherical mass. We will not attempt to apply general relativity to black holes, although no harm can be done by taking a peek at some of the equations which describe the space-time around a black hole. Special relativity describes a distance measure known as a metric which is invariant under Lorentz transformation:
![]()
In spherical coordinates, the metric is given by:
![]()
Under Einstein's theory, this invariant flat metric "changes" when there is mass present, and the metric becomes curved. Schwarzschild's accomplishment was to derive the metric surrounding a spherical mass, which became known as the Schwarzschild metric:
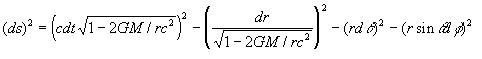
The most noticeable feature of this equation is that it has two terms dependent on the mass of the spherical object which modify the metric. This metric is now used to describe the space-time around a non-rotating, uncharged black hole. This equation is rather abstract upon first consideration, so perhaps examining how time changes near a massive object would yield more immediate and useful information. Just as moving clocks run slow, time passes more slowly in proximity to massive objects. If a clock is at rest at a distance r from an object, then the proper time dT it reads is given by:
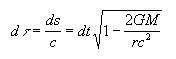
As M gets large, dT becomes much less than dt (the time that passes in a flat metric). This means that time passes more slowly closer to a massive object as judged by an observer further away from it. By combining equations (1) and (5), one can obtain the proper time at Rs, which turns out to be zero! From our vantage point a great distance away, nothing ever happens at Rs, as time does not pass at all. Even a photon emitted radially outward could not escape to infinity! The surface of a black hole at the Schwarzschild radius is known as the event horizon, as everything at a radius less than Rs is causally disconnected from the outside universe.
Using this definition of a black hole, it would seem preposterous that they would be able to radiate anything; even photons cannot leave such objects. However, our picture above has dealt only with the general relativistic characteristics of black holes, and has not examined the system using quantum mechanics. Indeed, until 1975, no one managed to formulate a cohesive theory of black holes that incorporated quantum mechanics. A young physicist named Stephen Hawking finally accomplished the feat, as he attempted to describe the space around a black hole in terms of quantum field theory. Unbelievably, the theory predicted that black holes should radiate particles at a steady rate!