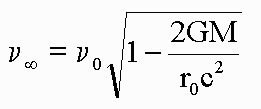

A approximation of the curvature near Earth can be done using elementary
trigonometry that results in an angular deflection of:

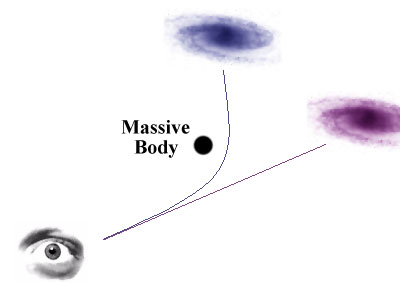 Since light must follow curved paths near massive bodies, the apparent
origin of light rays can be greatly affected. In the exaggerated
figure to the right, light from the blue object passes near a massive
object, such as a black hole, and is deflected towards the eye so that
it appears to originate from the 'virtual' lavender object. If there
is a smaller luminous object, such as a quasar, directly behind a
massive object, perhaps black hole but most likely something like a
galaxy, the light from the smaller object that might've passed out of
our field of view, can pulled and focused into apparent images of the
original object. The most famous of these gravitational lenses is the
Einstein Cross. (The four outer blobs on
the cross are the virtual images of one quasar behind a central galaxy.
Since light must follow curved paths near massive bodies, the apparent
origin of light rays can be greatly affected. In the exaggerated
figure to the right, light from the blue object passes near a massive
object, such as a black hole, and is deflected towards the eye so that
it appears to originate from the 'virtual' lavender object. If there
is a smaller luminous object, such as a quasar, directly behind a
massive object, perhaps black hole but most likely something like a
galaxy, the light from the smaller object that might've passed out of
our field of view, can pulled and focused into apparent images of the
original object. The most famous of these gravitational lenses is the
Einstein Cross. (The four outer blobs on
the cross are the virtual images of one quasar behind a central galaxy.

| Application of the Equivalence Principle as above in "The Bending of Light" to the scenario of photons directed radially along the classical field results in another prediction, that of gravitational frequency shift. This effect is mostly thought of in terms of redshift, since light leaving the areas of high curvature is of most interest and is redshifted. The equation which exactly describes frequency shift is below. If if photon is emitted at a distance r0 from a body of mass M, then the photon's frequency, at a far distance where the curvature is negligible, is shifted from its emitted frequency by the factor under the radical. Near Earth, as above, the effects of space-time on frequency are hardly observable(the frequency shift is on the same order as the angular deflection). Redshift near massive bodies is a different story. For all bodies, a photon emitted from the near Schwarzchild radius has its frequency reduced to almost zero. From the exact radius, the frequency observed is zero exactly; no light comes from Schwarzchild radius. The reason redshift is not observed in common experience is because of the small size of the Earth's Schwarzchild radius with respect to the surface of the Earth. |