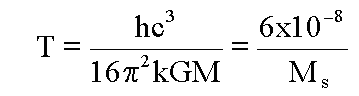Visual Appearances In Strong Gravitational Fields
"Black hole studies are a theorist's paradise but an observer's hell."
Imagine that your proposal to study a newly confimed black hole has been
accepted by the NSF(How could they deny you the grant money for
that?). In close orbit around the hole you will be able to witness
some of the more exotic manifestations of relativistic theory.
Fortunately, the trip to the hole is long enough for you to study up
on some of those theoretical predictions you may have forgotten.

|
One of the first direct consequences of the
Equivalence Principle
is the 'gravitating' of light towards massive bodies. A strict
interpretation of general relativity(GR) concerns paths in 4D
space-time, but from a visualizable 3D view, an apparent attractive
force
between mass and light results.
|
Thus it appears that light trajectories are deflected and distorted
by the enormous gravitational fields of massive bodies. The reality of this
prediction was confirmed in 1919 by Eddington, who measured deflection
around the Sun. Considering that the minimum mass for a black hole is
3 solar masses and the existence of supermassive black holes has been
postulated,
gravitational lensing
of light near these dark objects can, in principle, be much larger.
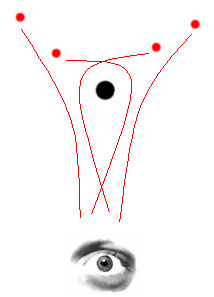
An interesting extension of the gravitational lensing of one object is
the possible lensing of all 'optically' near objects into a halo. The
image shows (with horrendous exaggeration) some of the possible photon
trajectories from a few luminous bodies around a black hole. If
perhaps you were observing a black hole closeby with a dense stellar
background, then a sizable halo might be observed. The following
movie shows calculations of curvature and lensing done on super
computers illustrating this effect.
|
|

Supposing that your spaceship is outfitted with a dazzling array of
probes and scientific gadgets, you begin writing your report early by
considering what effects on these you expect to observe. Say, for
instance, that aboard your ship is a gravimeter probe that can measure
the local acceleration (Exactly what the probe does is irrelevant as
long as it sends back information. The gravimeter is just an
example). The behavior of the returned signal(light) in curved space-time is
obviously important. Curvature has a more important effect on light,
however, than the mere re-direction discussed above. Relativity
predicts that light loses energy, i.e.
redshifts
, when its motion opposes the curvature. In 3D, this means that a
gravitational field reduces the frequency of light passing out of it.
The primary (only?) means of communication is through light signals
from the probe, so the dilation of the light is of importance.
Luckily, you remembered your relativistic corrections for redshift so
the signals from the probes will be useful for a while.
|
Musing over the list of experiments to perform, you remember some of
the sensational theoretical work of Stephen Hawking. The fact that
there is no accepted full blown theory of quantum gravity in existence
has not kept physicists from attempting to fuse the two in some
manner. Utilizing quantum mechanics and relativity, Hawking was able
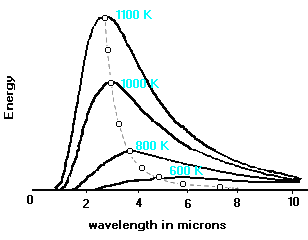
to show that black holes should appear as though they are emitting
thermal radiation that displays black-body behavior. The figure to the
right displays black-body radiation characteristics. The temperature
parameter of black-body radiation is the most interesting since it
describes the overall shape of the intensity curve and specifies the
peak of the thermal radiation.
|
Hawking's result (see
this page
for in-depth look at Hawking radiation) was that a black hole of mass
M would emit the thermal radiation at the temperature:
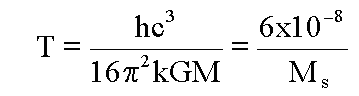 where Ms is the mass of the hole in solar masses. The striking
feature of this equation is the fact that the black hole must have
a tiny mass for appreciable temperatures.
where Ms is the mass of the hole in solar masses. The striking
feature of this equation is the fact that the black hole must have
a tiny mass for appreciable temperatures.
The total energy of the hole must be decreasing since some energy is
being given off in the form of radiation. Hawking also derived the
equation for the time it would take for a black hole to evaporate,
lose all of its energy, by Hawking radiation. The minimum time for a
black hole formed by stellar collapse (M ~ 3Ms) to evaporate turned
out to be roughly 10^67 years. Considering that the universe is
believed to only be 10^20 years old, only holes with mass one thousand
of a billionth of the Earth's mass could be currently evaporating. It
is postulated that some miniscule black holes may have been formed in
the Big Bang and should be in the final, detectable, explosive stages
of evaporation now, but none have been observed.