How Laplace's Equation was Solved in the Lecture Example
In Lecture #5, we saw how Laplace's Equation gives rise to the phenomenon
of electrostatic shielding by a conducting enclosure. We also asserted that
although this result is rigorously true for completely enclosed
cavities, the shielding is rather effective even for partially enclosed
regions.
As evidence of this we looked at a numerical solution to Laplace's Equation for
the case of a grounded metal cylinder with a variable-sized opening in its side.
You can view these solutions (along with isolated charges for comparison) by following these
links:
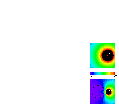 Cylinder with 30 degree opening
Cylinder with 30 degree opening
This image shows two panels, with potential plotted as a color contour map.
The top panel shows a charge alone, and thus has spherical symmetry. The lower
panel shows the field with the addition of a grounded cylinder with an opening
in its side. In addition to noting the shielding effect, you'll see that the
influence of the conductor at V=0 is to cause the equipotentials to "shrink"
about the source charge.
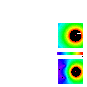 Cylinder with 180 degree opening
Cylinder with 180 degree opening
This pair of panels is similar, except that the cylinder now has a gaping wide
180 degree opening in it. Although the effect is far from perfect, there is a
surprisingly good degree of shielding within the shell concavity.
Each year, I
get an inquiry or two from students who want to know about the
technique used to generate these solutions. The following is a very brief
explanation, describing the numerical solution method, followed by a listing of
the C program that was used:
Laplace's equation is a second order partial differential equation, and in
order to solve it, you must find the unique function who derivatives satisfy
(del squared) V = 0, and simultaneously satisfies the required boundary
conditions. While a clever enough person might find an analytic solution in a
situation with a high degree of symmetry, for an irregularly shaped
configuration it is probably hopeless.
In such a case, we turn to finding an approximate solution by numerical
means. In this case, we use a method called finite differences . The main
idea is fairly simple. Instead of trying to find V at every point in
our domain, we'll seek to find V at a finite number of points that make up a
lattice or grid, which covers our region of interest. Then to calculate
"derivatives" of our function V, we'll approximate them by linear slopes
between neighboring grid points. For example, if we know V at two neighboring
points, V(i) and V(i+1), then the derivative there is approximately,
( V(i+1) - V(i) ) / delta_x . Similarly, we can use other neighbors to
approximate the second and third derivatives, and so on, as needed.
Now in the case of the two-dimensional Laplace equation, if we write it in
finite difference form, it comes out something like:
4 V(i,j) - V(i-1,j) - V(i+1,j) - V(i,j-1) - V(i,j+1) = 0
A brief examination of this equation shows that for any point (i,j), the value
of V there must be the average of the values of its four nearest
neighbors. So we can find a solution by iteratively passing through the
points of the grid and forcing them to satisfy this condition. We begin by
fixing the values of any boundary conditions, and prohibiting them from
changing. Then we sweep through the grid one point at a time, replacing V at
each point by the average of its neighbors. By repeating this process, the
solution "relaxes" toward the correct solution and eventually stops changing,
at which point we are done.
Below is a C source code listing for the program used to accomplish this in
the present example. The program is very bare bones, with no provisions for
error checking or checking for convergence, but it got the job done. I hope
you find it helpful.
/* laplace2.c - solves Laplace's eqn. in a grounded box
near a cylindrical shell with a variable sized opening
*/
#include <stdio.h>
#include <math.h>
main(argc,argv)
int argc ;
char *argv[] ;
{
FILE *infile , *outfile ;
float v[400][400] ;
int active[400][400] ;
int i , j , pass ;
float theta , fi , fj ;
infile = fopen(argv[1],"r") ;
outfile = fopen(argv[2],"w") ;
fscanf(infile,"%f",&theta) ;
printf("Shell half-angle: %f\n",theta) ;
/* initialize */
for(j=0;j<400;j++)
{
for(i=0;i<400;i++)
{
fi = (float) i ;
fj = (float) j ;
if(i==0 || i==399 || j==0 || j==399)
{
active[i][j] = 0 ;
v[i][j] = 0.0 ;
}
else if( ((fi-180.)*(fi-180.)+(fj-200.)*(fj-200.) < 675.0) &&
((fi-180.)*(fi-180.)+(fj-200.)*(fj-200.) > 575.0) &&
((180.-fi)/sqrt((fi-180.)*(fi-180.)+(fj-200.)*(fj-200.))) >
cos(theta*3.14159/180.) )
{
active[i][j] = 0 ;
v[i][j] = 0.0 ;
}
else if(i==220 && j==200)
{
active[i][j] = 0 ;
v[i][j] = 100.0 ;
}
else
{
active[i][j] = 1 ;
v[i][j] = 0.0 ;
}
}
}
/* do 10000 Gauss-Seidel updates */
printf("Starting updates...\n") ;
for(pass=0;pass<10000;pass++)
{
if((pass % 1000) == 0) printf("pass = %d\n",pass) ;
for(j=0;j<400;j++)
{
for(i=0;i<400;i++)
{
if(active[i][j] == 0) continue ;
else v[i][j] = 0.25 * (v[i][j-1]+v[i][j+1]+v[i-1][j]+v[i+1][j]) ;
}
}
}
/* write the output */
printf("Printing output...\n") ;
fprintf(outfile,"100 100\n") ;
fprintf(outfile,"5.0 0.0\n") ;
for(j=150;j<249;j++)
fprintf(outfile,"%f\n",(float)j) ;
fprintf(outfile,"\n") ;
for(i=150;i<249;i++)
fprintf(outfile,"%f\n",(float)i) ;
fprintf(outfile,"\n") ;
for(j=150;j<249;j++)
{
for(i=150;i<249;i++)
{
fprintf(outfile,"%f\n",v[i][j]) ;
}
}
fclose(infile) ;
fclose(outfile) ;
}
Return to Physics 51 Home Page
Last updated 9/13/95.
 Cylinder with 30 degree opening
Cylinder with 30 degree opening